A spherical balloon of radius ^@ 15 ^@ feet subtends an angle ^@ | Math Question and Answer

Answer:

$15 \sqrt{ 2 } \text{ feet }$

Step by Step Explanation:

The following picture shows the observer at point $A,$ observing a balloon.
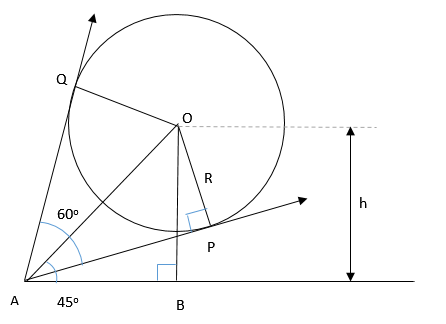
Let's assume the height of the center of the balloon to be $h,$ therefore $OB = h$
Also, assume the distance of center of the balloon from observer to be $D,$ therefore $OA = D$
For triangle $\triangle OAP,$
$\begin{align} & sin \angle OAP = \dfrac{ R } { D } \\ \implies & \dfrac{ sin 60^\circ } { 2 } = \dfrac{ R } { D } \\ \implies & sin 30^\circ = \dfrac{ R } { D } \\ \implies & \dfrac{ 1 }{ 2 } = \dfrac{ R }{ D} \\ \implies & D = 2R && \ldots (1) \end{align}$
For $\triangle AOB,$
$\begin{align} & sin \angle OAB = \dfrac{ h } { D } \\ \implies & sin 45^\circ = \dfrac{ h } { D } \\ \implies & { \dfrac{ 1 } { \sqrt{ 2 } }}^\circ = \dfrac{ h } { D } \\ \implies & D = \sqrt{ 2 } h && \ldots (2) \end{align}$
On equating two values of $D$ from equation $(1)$ and $(2),$
$\begin{align} & \sqrt{ 2 }h = 2R \\ \implies & h = R \sqrt{ 2 } \\ \implies & h = 15 \sqrt{ 2 } \text{ feet } \end{align}$

You can reuse this answer
Creative Commons License