Two circles of radii 13 cm and 5 cm intersect at two points and the distance between their centres is 12 cm. Find the length of the common chord.
- Home
- Math
- All Questions
Answer: 10 cm
Step by Step Explanation: - Take a look at the following image:
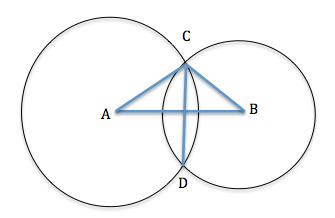
Here, A is the center of the first circle and B the center of the second circle. The common chord is CD.
Join AD and BD. Now, consider ∠ABC and ∠ABD. We have,
AC = AD (Radius of the circle with centre A)
BC = BD (Radius of the circle with centre B)
AB = AB (common)
Hence, ∠ABC ≅ ∠ABD by SSS.
So, ∠AOC = ∠AOD by CPCT. Also, AO = OB and CO = DO by CPCT.
Also, ∠AOC + ∠AOD = 180° (angles on a straight line)
⇒ ∠AOC + ∠AOC = 180°
⇒ 2 × ∠AOC = 180°
⇒ ∠AOC = 90°
Now, we know that the line AB bisects CD, and is perpendicular to it.
Also, the perpendicular from C to AB is half the length of CD. Let us call this length as L.
Area of ΔABC = × AB × L - By Heron's formula, area of ΔABC = ^@ \sqrt{ S(S-a)(S-b)(S-c) } ^@,
where, S = = = 15 cm
and a,b, and c are the length of three sides of the triangle.
So, area of ΔABC = ^@ \sqrt{ 15(15-13)(15-5)(15-12) } ^@ = 30 cm - Area of ΔABC = 30 cm = × AB × L = × 12 × L
Therefore, L = = 5 cm
Length of CD = 2L = 2 × 5 cm = 10 cm

 Jamaica
Jamaica
